4학년 2학기는 1학기에서 배운 내용을 토대로, 수학 개념을 한층 더 확장하고 심화하는 시기입니다. 삼각형과 사각형의 성질, 다각형과 대각선, 꺾은선그래프, 혼합 계산, 어림셈, 분수의 곱셈, 소수의 덧셈과 뺄셈 등이 주요하게 다뤄집니다. 아이들이 점점 더 추상적인 개념을 접하는 시기로, 수학적 사고력의 기초를 단단히 다지는 것이 중요합니다.
특히 4학년 2학기는 앞 학년에서 배운 직선·각·사각형에 대한 개념을 바탕으로 다각형과 대각선으로 확장하며, 표·그림그래프에서 꺾은선그래프로 발전합니다. 또한 분수와 소수를 처음 활용하던 단계에서 실제 계산으로 확장되면서, 수 연산의 큰 전환점을 맞이합니다.
방학은 아이가 여유 있게 쉬는 시간이지만, 동시에 1학기에서 부족했던 부분을 채우고 2학기를 준비할 수 있는 중요한 기회입니다. 이 시기를 잘 보내면 5학년의 분수·소수의 곱셈과 나눗셈, 도형의 넓이 구하기 등의 학습을 훨씬 수월하게 받아들일 수 있고, 반대로 놓치면 학년이 올라갈수록 수학에 대한 부담이 더 커질 수 있습니다.
수학은 나선형 학습입니다
수학은 한 번 배운 내용을 다음 단계로 이어가는 구조를 가지고 있습니다. 같은 주제를 학년마다 반복하지만, 범위와 깊이가 점점 넓어집니다.
수 개념
- 3학년 2학기: 분수의 활용, 소수와 연결
- 4학년 2학기: 분수와 소수의 덧셈과 뺄셈 (분수와 소수의 계산으로 확장)
곱셈과 나눗셈
- 3학년 2학기: 곱셈·나눗셈 확장, 몫과 나머지까지 구하기
- 4학년 2학기: 분수의 곱셈 도입 전 단계로, 분수와 소수의 계산 기반 다지기
도형
- 3학년 2학기: 원의 성질(반지름, 지름, 원의 특징)
- 4학년 1학기: 각의 크기 재기, 직각·예각·둔각, 평행·수직 이해
- 4학년 2학기: 여러 가지 삼각형과 사각형의 성질, 다각형과 대각선 탐구
자료와 측정
- 2학년 2학기: 표와 그래프
- 3학년 2학기: 그림그래프, 들이와 무게
- 4학년 2학기: 꺾은선그래프 (시간의 흐름에 따른 변화 파악)
이처럼 4학년 2학기는 앞 단계의 기초를 바탕으로 분수와 소수의 연산을 본격적으로 다루고, 여러 가지 삼각형과 사각형의 성질, 다각형과 대각선, 꺾은선그래프 등으로 학습을 확장하는 중요한 시기입니다. 따라서 새로운 내용을 예습하기보다, 3학년 과정과 4학년 1학기에서 배운 기초가 잘 자리 잡았는지를 확인하는 것이 가장 중요합니다.
4학년 2학기 수학 단원별 정리
1단원. 분수의 덧셈과 뺄셈
(진분수) + (진분수) : 합이 1보다 작은 경우

(진분수) + (진분수) : 합이 1보다 큰 경우

(대분수) + (대분수) : 분수 부분의 합이 1보다 작은 경우

(대분수) + (대분수) : 분수 부분의 합이 1보다 큰 경우

(진분수) - (진분수)

(대분수) - (대분수) : 분수 부분끼리 뺄 수 있는 경우

1 - (진분수)

(자연수) - (분수)

(대분수) - (대분수) : 분수 부분끼리 뺄 수 없는 경우

3학년 2학기와의 연결
3학년 2학기에는 분모가 같은 분수의 크기를 비교하고, 대분수를 가분수로 바꾸는 방법을 배웠습니다. 또한 자연수와 분수를 함께 이해하며 분수의 기본 개념을 다졌습니다.
4학년 2학기에는 이를 바탕으로 분수끼리의 덧셈과 뺄셈, 대분수의 계산을 배우며 분수 연산의 기초를 다지게 됩니다.
점검 포인트
💜 분모가 같은 분수의 덧셈과 뺄셈을 정확히 계산하는지 확인합니다.
💜 합이나 차가 1보다 클 경우, 가분수를 대분수로 바꾸는 과정을 이해하는지 살펴봅니다.
💜 자연수와 분수, 대분수 사이를 자유롭게 변환할 수 있는지 점검합니다.
💜 그림이나 수직선을 활용해 분수의 덧셈·뺄셈을 시각적으로 설명할 수 있는지 확인합니다.
지도 방법
기초 확인: 3학년에서 배운 ‘분모가 같은 분수의 크기 비교’를 다시 다루며 기본기를 점검합니다.
시각 자료 활용: 도형 나누기, 색칠하기, 수직선 등을 통해 분수 계산 과정을 눈으로 확인하도록 지도합니다.
변환 연습: 대분수를 가분수로, 가분수를 대분수로 바꾸는 연습을 반복하여 자연스럽게 계산할 수 있도록 합니다.
실생활 연결: 피자 조각, 초콜릿 나누기, 길이 재기 등 생활 속 사례로 분수 계산의 필요성을 느끼게 합니다.
단계별 문제: 합이나 차가 1보다 작은 경우 → 1보다 큰 경우 → 대분수끼리의 계산으로 난이도를 점차 확장합니다.
2단원. 삼각형
이등변 삼각형, 정삼각형
두 변의 길이가 같은 삼각형을 이등변삼각형이라고 합니다. 정삼각형도 이등변삼각형입니다.

세 변의 길이가 모두 같은 삼각형을 정삼각형이라고 합니다.

이등변삼각형과 정삼각형의 관계
- 정삼각형은 두 변의 길이가 같으므로 이등변삼각형이라고 할 수 있습니다.
- 이등변삼각형은 항상 세 변의 길이가 같은 것은 아니므로 정삼각형이라고 할 수 없습니다.
이등변 삼각형의 성질
이등변삼각형은 길이가 같은 두 변에 있는 두 각의 크기가 같습니다.
반으로 접으면 완전히 포개어집니다.

겹쳐진 부분에 있는 두 변의 길이와 두 각의 크기가 같습니다.
➔ (변 ㄱㄴ)=(변 ㄱㄷ)일 때 (각 ㄱㄴㄷ)=(각 ㄱㄷㄴ)
정삼각형의 성질
정삼각형은 세 각의 크기가 모두 같습니다.
정삼각형 모양의 종이를 서로 다른 세 방향으로 접으면

모두 완전히 포개어지므로 세 각의 크기가 모두 같습니다.
➔ (변 ㄱㄴ)=(변 ㄴㄷ)=(변 ㄷㄱ)일 때
(각 ㄱㄴㄷ)=(각 ㄴㄷㄱ)=(각 ㄷㄱㄴ)
예각삼각형
세 각이 모두 예각인 삼각형을 예각삼각형이라고 합니다.
(예각: 각도가 0º보다 크고 직각보다 작은 각)

둔각삼각형
한 각이 둔각인 삼각형을 둔각삼각형이라고 합니다.
(둔각: 각도가 직각보다 크고 180º보다 작은 각)
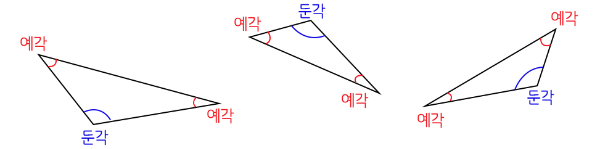
두 가지 기준으로 삼각형 분류하기

(1) 변의 길이에 따라 삼각형 분류하기
| 이등변삼각형 | 가, 나, 바, 아 |
| 세 변의 길이가 모두 다른 삼각형 | 다, 라, 마, 사 |
(2) 각의 크기에 따라 삼각형 분류하기
| 예각삼각형 | 직각삼각형 | 둔각삼각형 |
| 나, 라, 바 | 가, 사 | 다, 마, 아 |
(3) 변의 길이와 각의 크기에 따라 삼각형 분류하기
| 삼각형 | 예각삼각형 | 직각삼각형 | 둔각삼각형 |
| 이등변삼각형 | 나, 바 | 가 | 아 |
| 세 변의 길이가 모두 다른 삼각형 | 라 | 사 | 다, 마 |
1학기와의 연결
3학년 2학기에는 도형의 꼭짓점과 변을 중심으로 평면도형을 살펴보며, 삼각형이 세 개의 변과 꼭짓점으로 이루어진 도형임을 이해했습니다. 4학년 1학기에는 각의 크기를 배우면서 예각, 직각, 둔각의 개념을 익혔습니다.
2학기에는 이를 바탕으로 삼각형의 변과 각의 성질을 함께 고려하여, 이등변삼각형·정삼각형·예각삼각형·직각삼각형·둔각삼각형 등으로 분류하고 성질을 탐구합니다.
점검 포인트
💜 이등변삼각형의 성질(두 변과 두 각의 크기가 같음)을 이해하고, 대칭성을 설명할 수 있는지 확인합니다.
💜 정삼각형과 이등변삼각형의 관계를 이해하는지 살펴봅니다.
💜 예각·직각·둔각삼각형을 구분할 때, 각의 크기를 정확히 인식하는지 확인합니다.
💜 변의 길이와 각의 크기 두 가지 기준을 동시에 적용하여 삼각형을 분류할 수 있는지 점검합니다.
💜 삼각형의 분류 결과를 표로 정리하며 논리적으로 설명할 수 있는지 확인합니다.
지도 방법
기초 확인: 3학년에서 배운 꼭짓점·변 개념, 4학년 1학기 각의 종류를 다시 떠올리게 합니다.
종이접기 활동: 삼각형 종이를 접어 변의 길이와 각의 크기를 비교하며 성질을 발견하게 합니다.
시각 자료 활용: 눈금 종이, 삼각형 격자 등을 활용해 정삼각형·이등변삼각형을 직접 그려보고 확인하도록 지도합니다.
분류 활동: 삼각형을 ‘변의 길이 기준’과 ‘각의 크기 기준’으로 나누어 보고, 마지막에는 두 가지를 결합하여 종합적으로 분류하게 합니다.
실생활 연결: 건축물, 교량 구조, 교통 표지판 등 생활 속 삼각형을 찾아보고, 어떤 삼각형인지 분류하며 학습과 연결합니다.
3단원. 소수의 덧셈과 뺄셈
소수 두 자리 수

소수 두 자리 수의 각 자리 숫자가 나타내는 수
예) 5.63의 각 자리 숫자가 나타내는 수 알아보기
| 일의 자리 | 소수 첫째 자리 | 소수 둘째 자리 | |
| 5 | . | ||
| 0 | . | 6 | |
| 0 | . | 0 | 3 |
5.63에서 5는 일의 자리 숫자이고, 5를 나타냅니다.
6은 소수 첫째 자리 숫자이고, 0.6을 나타냅니다.
3은 소수 둘째 자리 숫자이고, 0.03을 나타냅니다.
➔ 5.63은 1이 5개, 0.1이 6개, 0.01이 3개인 수
소수 세 자리 수

소수 세 자리 수의 각 자리 숫자가 나타내는 수
예) 6.725의 각 자리 숫자가 나타내는 수 알아보기
| 일의 자리 | 소수 첫째 자리 | 소수 둘째 자리 | 소수 셋째 자리 | |
| 6 | . | |||
| 0 | . | 7 | ||
| 0 | . | 0 | 2 | |
| 0 | . | 0 | 0 | 5 |
6.725에서 6는 일의 자리 숫자이고, 6를 나타냅니다.
7은 소수 첫째 자리 숫자이고, 0.7을 나타냅니다.
2는 소수 둘째 자리 숫자이고, 0.02을 나타냅니다.
5는 소수 셋째 자리 숫자이고, 0.005를 나타냅니다.
➔ 6.725은 1이 6개, 0.1이 7개, 0.01이 2개, 0.001이 5개인 수
소수의 크기 비교
(1) 크기가 같은 소수
0.4와 0.40은 같은 수입니다. 필요한 경우 소수의 오른쪽 끝자리에 0을 붙여서 나타낼 수 있습니다.

(2) 소수의 크기 비교
자연수 부분, 소수 첫째 자리 수, 소수 둘째 자리 수, 소수 셋째 자리 수를 차례로 비교하여 높은 자리 수가 클수록 더 큰 수입니다.
예) 5.735 와 5.736 의 크기 비교 ➔ 5.735 < 5.736
| 자연수 비교 | 같으면 ➔ |
소수 첫째 자리 비교 | 같으면 ➔ |
소수 둘째 자리 비교 | 같으면 ➔ |
소수 셋째 자리 비교 |
| 5 . 7 3 5 | 5 . 7 3 5 | 5 . 7 3 5 | 5 . 7 3 5 | |||
| 5 . 7 3 6 | 5 . 7 3 6 | 5 . 7 3 6 | 5 . 7 3 6 |
(3) 자리 수가 다른 소수의 크기 비교
솟의 오른쪽 끝자리에 0을 붙여 자리 수를 같게 만든 다음 크기를 비교합니다.
예) 6.2 와 6.23의 크기 비교
6.2 = 6.20 이므로 6.20 < 6.23
소수 사이의 관계
(1) 1, 0.1, 0.01, 0.001 사이의 관계


(2) 소수 사이의 관계


소수 한 자리 수의 덧셈
예) 0.6 + 0.8 의 계산
① 전체 크기가 1인 모눈종이로 알아보기

➔ 0.6 + 0.8 = 1.4
② 0.1의 개수로 알아보기
0.6은 0.1이 6개이고 0.8은 0.1이 8개입니다.
0.6 + 0.8은 0.1이 6+8=14(개)이므로 1.4입니다.
③ 세로로 계산하기

- 소수점끼리 맞추어 세로로 씁니다.
- 같은 자리 수끼리 더합니다.
- 소수점을 그대로 내려 찍습니다.
소수 두 자리 수의 덧셈
예) 0.67 + 0.58 의 계산
① 전체 크기가 1인 모눈종이로 알아보기

➔ 0.67 + 0.58 = 1.25
② 0.01의 개수로 알아보기
0.67은 0.01이 67개이고 0.58은 0.01이 58개입니다.
0.67 + 0.58은 0.01이 67+58=125(개)이므로 1.25입니다.
③ 세로로 계산하기

- 소수점끼리 맞추어 세로로 씁니다.
- 같은 자리 수끼리 더합니다.
- 소수점을 그대로 내려 찍습니다.
# 소수점 아래 자리 수가 다른 소수의 덧셈
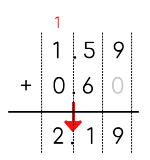
➔ 소수의 오른쪽 끝자리에 0이 있는 것으로 생각하여 자리 수를 같게 한 다음 더합니다.
소수 한 자리 수의 뺄셈
예) 1.5 - 0.8 의 계산
① 전체 크기가 1인 모눈종이로 알아보기

➔ 1.5 - 0.8 = 0.7
② 0.1의 개수로 알아보기
1.5는 0.1이 15개이고 0.8은 0.1이 8개입니다.
1.5 - 0.8은 0.1이 15-8=7(개)이므로 0.7입니다.
③ 세로로 계산하기

- 소수점끼리 맞추어 세로로 씁니다.
- 같은 자리 수끼리 뺍니다.
- 소수점을 그대로 내려 찍습니다.
소수 두 자리 수의 뺄셈
예) 1.72 - 0.95 의 계산
① 전체 크기가 1인 모눈종이로 알아보기

➔ 1.72 - 0.95 = 0.77
② 0.01의 개수로 알아보기
1.72은 0.01이 172개이고 0.95는 0.01이 95개입니다.
1.72 - 0.95은 0.01이 172-95=77(개)이므로 0.77입니다.
③ 세로로 계산하기

- 소수점끼리 맞추어 세로로 씁니다.
- 같은 자리 수끼리 뺍니다.
- 소수점을 그대로 내려 찍습니다.
1학기와의 연결
3학년 1학기에는 분수와 소수의 기초 개념을 처음 배웠습니다. 1/10을 0.1로, 1/100을 0.01로 나타내며, 소수 한 자리 수와 두 자리 수를 읽고 쓸 수 있게 되었습니다.
4학년 2학기에는 이를 바탕으로 소수의 범위를 넓혀 소수 세 자리 수까지 학습합니다. 소수의 자릿값을 더 깊이 이해하고, 소수의 크기를 비교하거나 덧셈·뺄셈 계산을 하며 소수의 기본 개념을 완성합니다.
점검 포인트
💜 소수의 자릿값(일의 자리, 소수 첫째 자리, 둘째 자리, 셋째 자리)을 구분할 수 있는지 확인합니다.
💜 같은 수라도 0.4와 0.40처럼 소수점 오른쪽에 0을 붙여 나타낼 수 있다는 사실을 이해하는지 살펴봅니다.
💜 소수를 크기 비교할 때 일의 자리부터 차례대로 비교할 수 있는지 확인합니다.
💜 소수를 10배 또는 1/10 했을 때 수의 자릿값이 이동하는 원리를 설명할 수 있는지 점검합니다.
💜 소수의 덧셈과 뺄셈을 할 때 소수점을 맞추어 계산할 수 있는지 확인합니다.
지도 방법
실물 관찰: 1m 자를 가져와 10cm, 1cm, 1mm 단위로 나누어 보면서 0.1, 0.01, 0.001과 연결시킵니다.
시각 자료 활용: 10칸, 100칸, 1000칸 모눈종이를 색칠하여 소수의 크기를 시각적으로 나타내게 합니다.
관계 이해: 1/10 = 0.1, 1/100 = 0.01, 1/1000 = 0.001임을 분수와 연결해 확인시킵니다.
탐구 활동: 소수를 더하고 빼는 과정을 색칠·조작 활동으로 표현해 보게 합니다.
정리 활동: 소수의 덧셈과 뺄셈은 반드시 ‘소수점을 맞추어 세로셈’으로 계산해야 함을 강조합니다.
4단원. 사각형
수직과 수선
두 직선이 만나서 이루는 각이 직각일 때, 두 직선은 서로 수직이라고 합니다.
두 직선이 서로 수직으로 만나면 한 직선을 다른 직선에 대한 수선이라고 합니다.

# 직선 뿐만 아니라 선분과 선분, 직선과 선분이 만나서 이루는 각이 직각일 때도 서로 수직이라고 합니다.
수선 긋기
(1) 삼각자를 사용하여 주어진 직선에 수직인 직선 긋기

① 삼각자의 직각을 낀 한 변을 주어진 직선에 맞춥니다.
② 삼각자의 직각을 낀 다른 한 변을 따라 직선을 긋습니다.
(2) 삼각자를 사용하여 한 점을 지나고 주어진 직선에 수직인 직선 긋기

① 삼각자의 직각을 낀 한 변을 주어진 직선에 맞춥니다.
② 삼각자의 직각을 낀 다른 한 변이 점 ㄱ을 지나도록 놓은 후 직선을 긋습니다.
평행과 평행선

- 한 직선에 수직인 두 직선을 그었을 때, 그 두 직선은 만나지 않습니다. 이와 같이 서로 만나지 않는 두 직선을 평행하다고 합니다
- 평행한 두 직선을 평행선이라고 합니다.
평행선 긋기
(1) 삼각자를 사용하여 주어진 직선과 평행한 직선 긋기
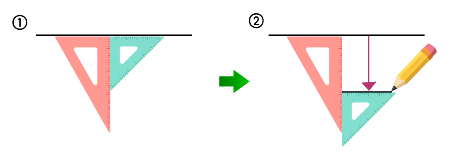
① 두 삼각자를 주어진 직선에 맞춥니다.
② 왼쪽 삼각자를 고정하고, 오른쪽 삼각자를 움직여 직선을 긋습니다.
(2) 삼각자를 사용하여 한 점을 지나고 주어진 직선과 평행한 직선 긋기

① 삼각자의 직각을 낀 변 중 한 변을 주어진 직선에 맞춥니다.
② 왼쪽 삼각자를 고정하고, 다른 삼각자가 점 ㄱ을 지나도록 맞추어 직선을 긋습니다.
# 한 직선과 평행한 직선의 수는 셀 수 없이 많이 그을 수 있습니다.
# 한 점을 지나고 한 직선과 평행한 직선의 수는 1개 뿐입니다.

평행선 사이의 거리
(1) 평행선 사이의 거리
평행선의 한 직선에서 다른 직선에 수직인 선분을 그었을 때, 그림과 같이 수직인 선분의 길이를 평행선 사이의 거리라고 합니다.

# 평행선 사이에 그은 선분 중 길이가 가장 짧은 선분은 수선입니다.
# 평행선 사이의 거리를 나타내는 선분의 길이는 모두 같습니다.
(2) 평행선 사이의 거리 재기
평행선의 한 직선에서 다른 직선에 수직인 선분을 긋고 그은 선분의 길이를 잽니다. ➔ 평행선 사이의 거리 : 5cm

(3) 평행선 사이의 거리가 주어진 평행선 긋기
예) 평행선 사이의 거리가 3cm가 되도록 주어진 직선과 평행한 직선 긋기

① 주어진 직선에서 3cm가 되는 곳에 점을 찍습니다.
② 왼쪽 삼각자를 고정하고, 다른 삼각자가 그 점을 지나도록 맞추어 직선을 긋습니다.
사다리꼴
평행한 변이 한 쌍이라도 있는 사각형을 사다리꼴이라고 합니다.

# 평행한 변이 있기만 하면 사다리꼴이므로 평행한 변이 2쌍 있는 사각형도 사다리꼴입니다. (직사각형, 정사각형)
평행사변형
마주 보는 두 쌍의 변이 서로 평행한 사각형을 평행사변형이라고 합니다.

평행사변형의 성질
평행사변형 모양의 종이를 선을 따라 자른 후 마주 보는 변끼리 겹쳐 보면 완전히 겹쳐집니다.

① 마주 보는 두 변의 길이가 같습니다.
② 마주 보는 두 각의 크기가 같습니다.
③ 이웃한 두 각의 크기의 합이 180º 입니다.
마름모
네 변의 길이가 모두 같은 사각형을 마름모라고 합니다.

마름모의 성질
① 마주 보는 두 각의 크기가 같습니다.
② 이웃한 두 각의 크기의 합이 180º 입니다.
③ 마름모 모양의 종이를 반으로 두 번 접었다 펼쳤을 때

- 마주 보는 꼭짓점끼리 이은 두 선분이 서로 수직으로 만납니다.
- 마주 보는 꼭짓점끼리 이은 두 선분은 서로의 길이를 반으로 나눕니다.
# 마름모는 마주 보는 두 쌍의 변이 서로 평행하여 평행사변형이 성질도 가지고 있습니다.
직사각형과 정사각형의 성질

- 직사각형과 정사각형은 마주 보는 두 쌍의 변이 서로 평행하고 네 각이 모두 직각입니다.
- 직사각형은 마주 보는 두 변의 길이가 같고, 정사각형은 네 변의 길이가 모두 같습니다.
사각형을 여러 가지 성질에 따라 분류하기

<사각형의 이름이 될 수 있는 것>
- 마주 보는 두 쌍의 변이 서로 평행하므로 사다리꼴, 평행사변형입니다.
- 네 변의 길이가 모두 같으므로 마름모입니다.
1학기과의 연결
3학년 1학기에는 직선·선분·반직선을 배우며 도형의 기본 틀을 익혔고, 4학년 1학기에는 각도를 재며 직각·예각·둔각을 구분하는 방법을 배웠습니다. 이러한 학습을 바탕으로 2학기에는 수직과 평행을 이해하고, 다양한 사각형의 성질을 탐구합니다.
점검 포인트
💜 두 직선이 직각을 이루면 수직임을 이해하고, 삼각자를 사용해 수직인 직선을 정확히 그릴 수 있는지 확인합니다.
💜 평행선의 의미를 알고, 주어진 직선을 기준으로 평행선을 바르게 그릴 수 있는지 살펴봅니다.
💜 사다리꼴·평행사변형·마름모·직사각형·정사각형의 성질을 구별하고, 공통점과 차이점을 비교할 수 있는지 확인합니다.
💜 같은 사각형이 여러 이름(예: 정사각형은 직사각형이면서 마름모)이 될 수 있음을 이해하는지 살펴봅니다.
지도 방법
구체적 도구 활용: 삼각자, 자, 종이 오리기·접기 활동을 통해 수직과 평행을 직접 경험하게 합니다.
시각 자료 연결: 교과서 삽화(사각형 모양, 평행선, 수직선 그림 등)를 활용하여 추상적 개념을 구체적으로 이해하게 합니다.
성질 탐구 활동: 사다리꼴·평행사변형·마름모 등 여러 사각형을 비교하며 성질을 정리하게 합니다.
거리 측정 활동: 평행선 사이의 거리를 자로 재어 보고, 수직인 선분이 두 직선 사이의 가장 짧은 길이임을 생활 속 사례와 연결합니다.
사각형 분류 정리: 사각형들을 성질에 따라 분류하고, 같은 도형이 여러 이름을 가질 수 있음을 도식화하여 이해를 확장시킵니다.
5단원. 꺾은선그래프
꺾은선그래프 알아보기
연속적으로 변화하는 양을 점으로 표시하고, 그 점들을 선분으로 이어 그린 그래프를 꺾은선그래프라고 합니다.
예)

① 가로가 나타내는 것: 연도
② 세로가 나타내는 것: 학생 수
③ 세로 눈금 한 칸의 크기: 2명
④ 꺾은선이 나타내는 것: 연도별 초등학생 수의 변화
⑤ 초등학생 수가 가장 많이 변한 시기: 2022년과 2023년 사이
물결선을 사용한 꺾은선그래프 알아보기
꺾은선그래프로 나타낼 때 물결선(~)을 사용하여 필요 없는 부분을 줄여서 나타내면 자료의 변화를 더 뚜렷하게 알 수 있습니다.
예)
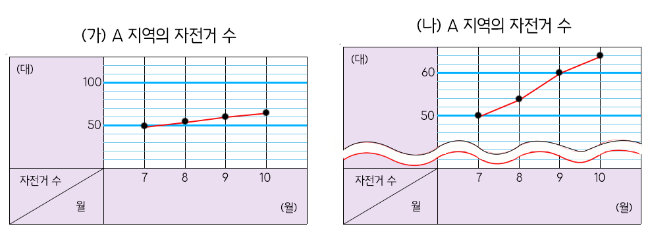
① (가) 그래프는 세로 눈금 한 칸을 10대로 나타냈습니다.
② (나) 그래프는 0대와 50대 사이를 물결선으로 줄이고 세로 눈금 한 칸을 2대로 나타냈습니다.
➔ (나) 그래프가 (가) 그래프보다 자전거 수의 변화를 더 뚜렷하게 알 수 있습니다.
③ 자전거 수가 점점 늘어나고 있으므로 11월에는 자전거 수가 10월보다 더 늘어날 것 같습니다.
꺾은선그래프로 나타내기
<꺾은선그래프로 나타내는 방법>
① 가로와 세로에 각각 무엇을 나타낼지 정합니다.
② 물결선을 넣을 부분과 세로 눈금 한 칸의 크기를 정하고, 조사한 수 중에서 가장 큰 수를 나타낼 수 있도록 눈금의 수를 정합니다.
③ 가로 눈금과 세로 눈금이 만나는 자리에 점을 찍고, 점들을 선분으로 잇습니다.
④ 꺾은선그래프에 알맞은 제목을 씁니다.
예) 어느 지역의 쌀 수확량을 조사하여 나타낸 표를 보고 꺾은선그래프로 나타내기
쌀 수확량
| 연도(년) | 2021 | 2022 | 2023 | 2024 |
| 수확량(kg) | 5200 | 5800 | 6600 | 7000 |

자료에 알맞은 그래프로 나타내기
<막대그래프와 꺾은선그래프의 비교>

| 막대그래프 | 꺾은선그래프 | |
| 같은 점 | - 가로는 요일, 세로는 횟수를 나타냅니다. - 세로 눈금 한 칸의 크기가 같습니다. |
|
| 다른 점 | -자료를 막대로 나타냈습니다. | - 자료를 점을 찍은 후 선분으로 이어 나타냈습니다. |
2, 3학년과의 연결
2학년 2학기에는 표와 그래프로 자료를 정리하며 기본적인 표현 방법을 익혔고, 3학년 2학기에는 그림그래프를 사용해 자료를 더 쉽게 읽고 비교하는 경험을 쌓았습니다. 이러한 배움을 바탕으로 4학년 2학기에는 시간이 흐르며 변하는 자료를 꺾은선그래프로 나타내고, 그 변화를 해석하는 방법을 탐구합니다.
점검 포인트
💜 가로와 세로축이 각각 무엇을 나타내는지 바르게 설명할 수 있는지 확인합니다.
💜 눈금 한 칸이 나타내는 크기를 정확히 파악하고, 자료를 알맞게 읽을 수 있는지 살펴봅니다.
💜 꺾은선이 나타내는 ‘변화의 흐름’을 이해하고, 가장 많이 변한 시기나 증가·감소 추세를 해석할 수 있는지 점검합니다.
💜 물결선을 사용하여 필요한 부분만 나타낸 꺾은선그래프를 읽고, 자료의 변화를 더 뚜렷하게 파악할 수 있는지 확인합니다.
💜 막대그래프와 꺾은선그래프의 공통점과 차이점을 구별하며, 어떤 자료에 더 적합한지 설명할 수 있는지 살펴봅니다.
지도 방법
구체적 경험 활용: 생활 속 자료(날씨 변화, 운동 시간, 물건 판매량 등)를 모아 꺾은선그래프로 나타내게 합니다.
시각 자료 연결: 교과서의 그래프 삽화와 실제 자료를 함께 비교하여, 표 → 그림그래프 → 꺾은선그래프로 확장되는 과정을 이해시킵니다.
변화 해석 활동: 그래프의 오르내림을 읽고 ‘가장 많이 증가한 시기’, ‘가장 크게 줄어든 시기’를 찾아보며 변화의 의미를 생각하게 합니다.
물결선 사용 연습: 필요 없는 부분을 줄여 나타내는 물결선의 의미를 실제 그래프에 적용해 보게 합니다.
그래프 비교 활동: 같은 자료를 막대그래프와 꺾은선그래프로 각각 나타내어 보고, 두 그래프의 특징을 비교하게 합니다.
6단원. 다각형
다각형
(1) 선분으로만 둘러싸인 도형을 다각형이라고 합니다.
(2) 다각형은 변의 수에 따라 변이 5개이면 오각형, 변이 6개이면 육각형, 변이 7개이면 칠각형, 변이 8개이면 팔각형이라고 부릅니다. (변의 수에 따라 다각형의 이름이 정해집니다.)
| 다각형 |  |
 |
 |
 |
| 변의 수(개) | 5 | 6 | 7 | 8 |
| 이름 | 오각형 | 육각형 | 칠각형 | 팔각형 |
# 다각형이 아닌 도형
① 굽은 선이 포함된 도형 ② 선분으로 완전히 둘러싸여 있지 않은 도형

정다각형
변의 길이가 모두 같고, 각의 크기가 모두 같은 다각형을 정다각형이라고 합니다.
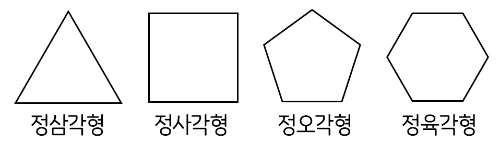
➔ 정삼각형은 변의 수가 가장 적은 정다각형입니다.
# 정다각형이 아닌 도형
① 변의 길이는 모두 같지만 각의 크기가 모두 같지는 않은 도형
② 각의 크기는 모두 같지만 변의 길이가 모두 같지는 않은 도형
대각선
(1) 다각형에서 선분 ㄱㄷ, 선분 ㄴㄹ과 같이 서로 이웃하지 않는 두 꼭짓점을 이은 선분을 대각선이라고 합니다.
(2) 대각선의 수
| 다각형 |  |
 |
 |
 |
| 대각선의 수(개) | 0 | 2 | 5 | 9 |
# 삼각형은 모든 꼭짓점이 서로 이웃하고 있어서 대각선을 그을 수 없습니다.
# 꼭짓점의 수가 많을수록 대각선의 수가 많습니다.
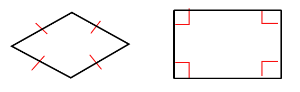
여러 가지 사각형의 대각선의 성질

① 두 대각선이 서로 수직으로 만나는 사각형: 마름모, 정사각형
② 두 대각선의 길이가 같은 사각형: 직사각형, 정사각형
③ 한 대각선이 다른 대각선을 똑같이 둘로 나누는 사각형: 평행사변형, 마름모, 직사각형, 정사각형
3학년과의 연결
3학년 1학기에는 직선·선분·반직선을 배우며 도형의 기본 요소를 익혔고, 4학년 1학기에는 각도의 크기를 재고, 직각·예각·둔각을 구분하며 도형에서 각의 의미를 확장했습니다.
4학년 2학기에는 삼각형과 사각형 단원에서 직각과 수직, 평행의 개념을 다루며 도형의 성질을 구체적으로 탐구했습니다. 이러한 학습을 바탕으로 이번 단원에서는 여러 변으로 이루어진 다각형으로 범위를 넓혀, 정다각형과 대각선의 성질까지 폭넓게 배우게 됩니다.
점검 포인트
💜 다각형과 다각형이 아닌 도형을 구별할 수 있는지 확인합니다.
💜 변의 수에 따라 오각형, 육각형, 칠각형, 팔각형의 이름을 바르게 말할 수 있는지 살펴봅니다.
💜 정다각형의 성질(변의 길이와 각의 크기가 모두 같음)을 이해하고, 정삼각형·정사각형과 연결할 수 있는지 점검합니다.
💜 대각선의 의미를 알고, 꼭짓점의 수에 따라 대각선의 개수가 달라짐을 설명할 수 있는지 확인합니다.
💜 여러 사각형의 대각선 성질(서로 수직, 길이가 같음, 다른 대각선을 이등분함 등)을 구체적으로 비교할 수 있는지 살펴봅니다.
지도 방법
구체적 도형 제시: 다양한 다각형 모형을 보여주고, 변의 수에 따라 이름 붙이기를 활동으로 이끕니다.
정다각형 탐구: 종이 접기·오리기를 활용해 정삼각형, 정사각형, 정육각형을 직접 만들어 보게 합니다.
대각선 활동: 다각형에 대각선을 직접 그려보며 개수를 세어보고, 사각형에서 대각선의 성질을 비교하게 합니다.
연계 학습 강조: 앞에서 배운 직각·수직·평행 개념이 다각형과 대각선 학습에 어떻게 활용되는지 연결 지어 설명합니다.
글을 맺으며
4학년 2학기는 1학기에서 다진 기초 위에 분수·소수의 연산, 도형의 성질, 자료 해석을 심화·확장하는 시기입니다. 분수와 소수의 덧셈·뺄셈은 통분과 소수 자릿값을 정확히 맞추는 연습이 핵심이며, 도형 단원에서는 여러 가지 삼각형과 사각형의 성질, 다각형과 대각선을 실제로 그려 보고 비교하면서 개념을 몸에 익히는 것이 중요합니다. 꺾은선그래프는 수량의 변화를 시간적 흐름 속에서 읽고 설명하는 힘을 기르게 합니다.
이 시기에는 ‘빠른 계산’보다 ‘논리적인 과정’이 강조됩니다. 분수·소수의 계산 절차를 단계별로 기록하는 습관, 삼각형·사각형의 성질을 근거로 설명하는 연습, 그래프를 통해 자료의 증감을 구체적으로 말하는 활동을 반복해야 합니다. 단순한 정답 찾기보다 왜 그렇게 계산했는지를 말로 설명하는 경험이 수학적 사고력을 크게 키워 줍니다.
가정에서는 매일 10~15분 정도, 분수와 소수 계산을 짧게 연습하거나 생활 속에서 그래프 읽기·도형 찾기 활동을 해 보세요. 작은 성취가 쌓일수록 5학년에서의 분수 곱셈·나눗셈, 복잡한 도형 학습으로 자연스럽게 이어집니다.
📚 함께 읽으면 좋은 글
[2022년 개정] 1학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비
[2022 개정] 1학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비
수학 교과에는 수와 연산, 도형, 측정, 규칙성, 자료와 가능성의 다섯 가지 영역이 있습니다. 교과과정은 이 영역들을 고르게 다루면서도, 학기별·학년별로 같은 주제를 반복하며 점차 심화해
jaramnamu.com
[2022년 개정] 2학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비
[2022 개정] 2학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비
2학년 2학기는 1학년과 2학년 1학기에서 다져온 기초를 바탕으로, 수학 개념을 한 단계 더 확장하는 시기입니다. 특히 네 자리 수(몇천까지), 곱셈 활용, 시·분 단위의 시각 계산, 도형의 대칭과
jaramnamu.com
[2022년 개정] 3학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비
3학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비
3학년 2학기는 1학기에서 배운 내용을 토대로, 수학 개념을 한 단계 더 확장하는 시기입니다. 곱셈과 나눗셈의 심화, 원의 성질, 분수의 활용, 들이와 무게, 그림그래프가 주요하게 다뤄집니다.
jaramnamu.com
'초등 학습 길잡이' 카테고리의 다른 글
| 5학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비 (1) | 2025.10.23 |
|---|---|
| [2022 개정] 3학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비 (17) | 2025.09.01 |
| [2022 개정] 2학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비 (52) | 2025.08.18 |
| [2022 개정] 1학년 2학기 수학, 이렇게 준비하세요 | 단원별 핵심 정리와 학습 준비 (48) | 2025.08.15 |
| 받아쓰기, 어떻게 해야할까? | 3가지 학습 유형과 추천 교재 (41) | 2025.08.14 |



